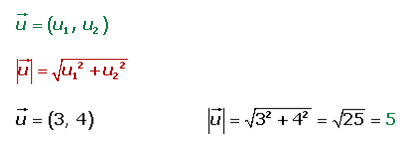Los vectores en el álgebra lineal

Al igual que las matrices y los sistemas de ecuaciones lineales, los vectores son claves en el estudio del álgebra lineal. Aunque el concepto de vector presenta múltiples acepciones, en matemáticas lo entendemos como una magnitud física de longitud (módulo) y orientación (dirección) determinada que está representada geométricamente como segmentos de recta. ¿Quieres saber cuál es el papel de los vectores en el álgebra lineal? Presta especial atención.

¿Qué es un vector?

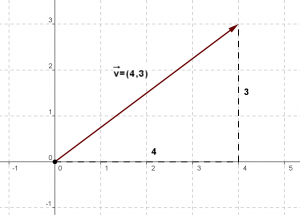
En el mundo de la geometría, un vector es una expresión geométrica que se extiende desde un punto de referencia llamado origen, hacia otro punto que se denomina extremo. El concepto de vector hace referencia a la idea de desplazamiento en el espacio desde un espacio inicial a un espacio final.

La definición de vector puede ser incluso más sencilla: todo segmento de recta que está dirigido en el espacio. Los vectores se definen con los puntos que ocupan su origen y extremo en los ejes de coordenadas. Los vectores se encuentran definidos por los componentes de módulo, dirección, sentido y punto de aplicación. Vamos a verlos con más detenimiento.

Componentes de los vectores

Como ya hemos adelantado, todos los vectores poseen una serie elementos que los definen:

• Dirección: hace referencia a la dirección de la recta en la que se encuentra el vector, o cualquier recta paralela.
• Sentido: es el sentido hacia donde se dirige el segmente. Es el lugar al que indica desde el origen hasta el extremo del vector. El sentido del vector se señala con una flecha.
• Punto de aplicación: es el lugar exacto del plano donde se sitúa el vector.
• Módulo: también es la longitud del segmento que representa el vector.

Para calcular el módulo de un vector debemos realizar una serie de cálculos muy sencillos que nos permitirá saber cuánto mide su longitud. El módulo de un vector es igual a la raíz de la suma de los cuadrados de sus componentes. Presta especial atención:

Esta es la fórmula del módulo de un vector, y además, te dejamos un ejercicio resuelto de modulo de vector con el que podrás conocer cuánto mide un vector.

Tipos de vectores en álgebra lineal

Aquí podemos ver la clasificación de los vectores que te puedes encontrar dependiendo del grado de equivalencia:

• Vectores equipolentes: son dos vectores que poseen el mismo módulo, dirección y sentido.
• Vectores libres: es un grupo de vectores equipolentes. Es decir que comparten módulo, dirección y sentido.
• Vectores ligados: son vectores equipolentes, y que además se encuentran en la misma recta.

Aquí puedes ver otros tipos de vectores:

• Vectores opuestos: los vectores opuestos tienen el mismo módulo, dirección, pero con distinto sentido.
• Vectores unitarios: son los vectores que su módulo es igual a 1.
• Vectores concurrentes: los vectores concurrentes comparten el mismo punto de origen.
• Vectores de posición: poseen su punto de origen en el punto 0 de coordenadas
• Vectores paralelos: estos vectores se encuentran en rectas paralelas del plano.
• Vectores ortogonales: son los vectores perpendiculares. Su producto escalar es cero.
• Vectores ortonormales: son dos vectores unitarios (módulo = 1), cuyo productos escalar de estos vectores es 0. Es decir dos vectores unitarios y perpendiculares.