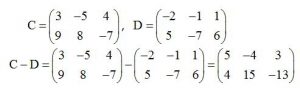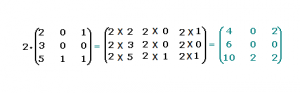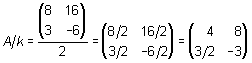¿Cómo se resuelven las operaciones con matrices?

Ahora que conocemos los distintos tipos de matrices que existen y el papel que juegan sus estructuras de filas y columnas en el álgebra lineal, vamos a ver cómo se resuelven las operaciones con matrices de manera fácil y sencilla. Los ejemplos de matrices que te proponemos a continuación son de lo más ilustrativos. ¿Les echamos un vistazo?

Operaciones con matrices

En el mundo de las matrices también encontramos las operaciones más tradicionales. Aquí podrás ver los tipos de operaciones con matrices, suma, resta, multiplicación y división, y las diferentes características y procesos de resolución que poseen cada una de ellas. Seguro que los ejercicios resueltos de operaciones con matrices te ayudan a que entiendas perfectamente el camino a seguir encontrar la solución.

Suma de matrices

Para realizar la suma de matrices debemos sumar los números que se encuentren en el mismo lugar. El resultado de esta operación da lugar a una nueva matriz que surge de sumar sus componentes. En este ejercicio de suma de matrices puedes ver perfectamente cómo se realiza paso a paso.

Resta de matrices

El procedimiento para restar matrices es el mismo que hemos comentado anteriormente para la suma. En la diferencia de matrices también debemos restar cada uno de los número que se encuentren en la misma posición. Aquí tienes el ejemplo que te ayudará a resolver es tipo de operaciones con matrices.

Multiplicación de matrices

Existen diferentes situaciones en las que nos podemos encontrar una multiplicación con una matriz. Descubre los mecanismos de estas operaciones con matrices con ejemplos para que puedas entender paso a paso cómo resolver operaciones con matrices.

Multiplicación de un escalar por una matriz

Las operaciones de un número por una matriz se resuelven de una manera muy fácil, ya que tan sólo debemos multiplicar el número por cada uno de los componentes de la matriz. El resultado que obtenemos es una única matriz, producto de la operación realizada.

Multiplicación de una matriz por otra matriz

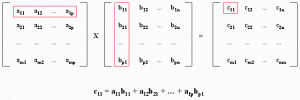
Lo primero que debemos saber es que dos matrices sólo son multiplicables, si el número de columnas de la primera matriz se corresponde con el número de filas de la segunda.

Para calcular el producto de una matriz tenemos que multiplicar cada componente de la primera fila de la matriz A, por cada uno de los componentes de la primera columna de la matriz B y luego sumarlos. Después multiplicamos la segunda fila por todos los elementos de la primera columna de la otra matriz, y los sumamos. Así sucesivamente hasta que consigamos crear otra matriz resultante de la multiplicación de matrices.

Aunque a priori pueda parecer muy complicado, calcular el producto de matrices es muy sencillo. Si te parece que es un poco enrevesado, aquí podemos un ejercicio resuelto con el poder comprender perfectamente el método para multiplicar matrices.

Cabe destacar que en la matrices el orden de los factores sí que altera el producto. Esto quiere decir que el resultado de multiplicar A x B no será el mismo que el de multiplicar B x A.

División de matrices

Para dividir una matriz entre un número debemos dividir cada uno de los componentes de la matriz entre el número que se encuentra en el divisor. En el ejemplo puedes ver perfectamente cómo se realiza la división de matrices, con el mismo mecanismo que el de multiplicar una matriz por un número.

Las divisiones de matrices, no están definidas como tales en las matemáticas. Para realizar la división entre matrices, entendida como la operación contraria a la multiplicación, debemos multiplicar la matriz natural por la inversa de esta matriz. De forma que podemos decir que la división de matrices es igual a producto de una matriz por su inversa (A x A^-1). Para ello, debemos calcular la inversa de una matriz, y después realizar la multiplicación como hemos hecho anteriormente.