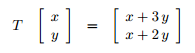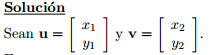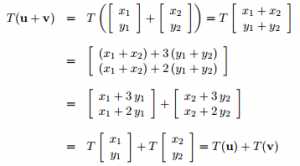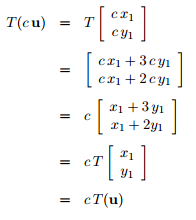Las transformaciones lineales, también conocidas como aplicaciones lineales o funciones lineales, son funciones comprendidas entre dos espacios vectoriales. Conocer y entender el concepto de vector -así como el papel de éste en el álgebra lineal- será vital para analizar la función de las transformaciones lineales en el álgebra lineal. ¿Quieres saber por qué? No dudes en seguir leyendo.
Elementos de las transformaciones lineales
Las transformaciones lineales son una parte de las matemáticas aplicable en el mundo cotidiano. Se trata de un conjunto de reglas y relaciones que sirven para cambiar el tamaño o la dirección de un vector que está dentro de un espacio vectorial. Esta parte del álgebra lineal es compleja y es mejor definir cada uno de los conceptos primero:
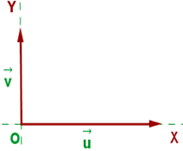
- Los vectores en álgebra lineal son expresiones geométricas. Un vector es un punto que parte en forma de línea hacia una dirección, lo podrías imaginar como una flecha. Va de un punto fijo (O) hasta un extremo (Y).
- Un escalar son los elementos de un cuerpo, normalmente se definen con números.
- Un espacio vectorial es el conjunto de vectores (v+u), un conjunto de escalares, y dos operaciones. Sus elementos se pueden sumar y multiplicar por escalares mediante funciones mientras que conserven esa estructura. Estas funciones se llaman también transformaciones lineales.
Aplicaciones de las transformaciones lineales
Para llevar a cabo la aplicación de las transformaciones lineales debemos saber que nos sirven para modificar vectores, estrechar y agrandar formas en línea recta. Y que son funciones lineales, es decir, que preservan las operaciones en el espacio vectorial.
Hablando en términos matemáticos, si un espacio vectorial 'V' queremos transformarlo a 'U', cuyos vectores son 'u' y 'v' y escalar 'c'. La tranformación (T) del espacio vectorial 'V' al 'U', sólo va a ser lineal si se cumplen las siguientes propiedades de la transformación lineal. Veamos la fórmula:
T(u+v)= T(u)+T(v)
T(cv)=cT(u)
Ejemplos de transformaciones lineales
Para entender mejor en que consisten las funciones lineales en álgebra te mostramos un ejemplo resuelto con un caso en el que tenemos que aplicar las dos propiedades -suma y multiplicación de escalar-.
Para determinar si la tranformación T= R²→R² es lineal, primero comprobamos la suma:
Dado que es una transformación lineal seguimos con la fórmula:
Ahora, scomprobamos si se cumple la condición con el escalar (c):
Como se cumplen las dos condiciones podemos definir con seguridad que T: R²→R², es lineal.