¿Cuántos tipos de matrices existen en el álgebra?

Ya sabemos que las matrices son conjuntos de elementos que están ordenados en estructuras de filas y columnas -y que dependiendo del número de filas y columnas que posea una matriz, estaremos hablando de una dimensión u otra-. Pero, ¿cuántos tipos de matrices existen en el álgebra? ¿Hasta qué punto influye la forma de estos conjuntos en la clasificación de las matrices en el álgebra lineal? Descúbrelo con nosotros.

Tipos de matrices en álgebra lineal

Existen muchos tipos de matrices en álgebra lineal. Recordamos que las matrices se utilizan para organizar datos en matemáticas, se componen de valores dispuestos en una estructura de filas y columnas. Estos valores pueden ser número o letras, ya que pueden ser ecuaciones u otras matrices. Las cantidades que aparecen dentro de las filas y columnas pueden sumarse, multiplicarse y descomponerse de varias maneras.

La clasificación de matrices se establece a partir de cómo se organizan sus valores en las filas y columnas, para abarcar todas las posibilidades existe una larga lista, Entonces, ¿cuáles son los tipos de matrices en matemáticas? Empecemos una por una: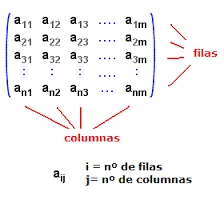

Matriz fila

Se dice que es un matriz de este tipo cuando se forma por una única fila.

Matriz columna

La matriz columna, como su nombre indica tiene sólo una columna.

Matriz rectangular

Este tipo de matriz algebraica tiene una cantidad de filas y columnas diferente. Puede ser horizontal o vertical.

Una matriz horizontal, sería aquella que tiene más columnas que filas. Y, una matriz vertical es aquella que tiene más filas que columnas.

Matriz nula

Esta matriz se da cuando todos sus elementos son ceros.

Matriz cuadrada

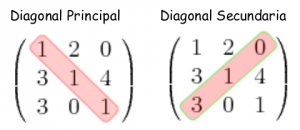
La matriz cuadrada tiene la misma cantidad de filas que de columnas. Los valores que van desde la esquina superior izquierda hacia la inferior derecha, forman una diagonal que se llama diagonal principal, la contraria, se llama diagonal secundaria.

Matriz triangular

Esta clasificación de matrices algebraicas es más específica. Decimos que es una matriz triangular superior cuando observamos que los números debajo de la diagonal principal son ceros. Y, matriz triangular inferior cuando se da al revés, que los números por encima de la diagonal principal son ceros.

Matriz diagonal

Esta matriz es una matriz cuadrada en la que todos los números, inferiores y superiores, a la diagonal principal son nulos.

A su vez, podemos clasificar estas matrices en matemáticas en dos más: matriz escalar que es cuando se dan las características de una matriz diagonal y a su vez los elementos de la diagonal principal son iguales. Y, matriz de identidad o unidad, cuando los elementos de la diagonal principal son iguales a 1.

Matriz traspuesta

Se llama matriz traspuesta a la matriz cuadrada que se obtiene al cambiar las filas y columnas de a otra de manera ordenada. Pasamos de una matriz A a una matriz Aⁿ.

Matriz regular

Una matriz regular es una matriz invertible, tiene inversa una matriz cuadrada.

Matriz singular

Es una matriz cuadrada, pero no tiene matriz inversa.