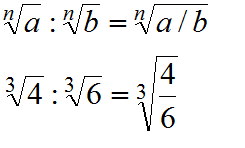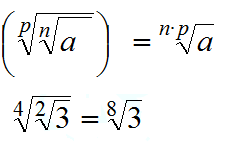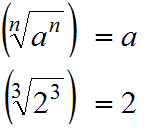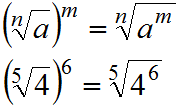En ocasiones, los radicales y potencias se presentan con formas complejas que nos complican su resolución. Sin embargo, debemos saber que las raíces poseen muchas formas equivalentes que nos ayudan a plantear problemas de forma diferente. Para ello, es necesario conocer las propiedades de los radicales que nos permitirán realizar las diferentes operaciones que nos conducirán al resultado final. Los ejemplos y ejercicios de propiedades con radicales te ayudarán a comprender cómo funcionan estas operaciones.
Propiedades de las raíces
Las propiedades de los radicales nos permiten trabajar con ellos para intentar resolver operaciones con radicales que, a priori, parece difícil encontrar la solución. Estas propiedades de las raíces también nos sirven para simplificar los radicales al máximo, y reducirlos hasta que ofrezcan una forma más sencilla.
Producto de raíces
La raíz de un producto es igual al producto de la raíz de cada uno de los factores.
Cociente de radicales
La división de radicales es igual a la raíz del numerador entre la raíz del denominador.
Raíz de un radical
La raíz de una raíz da lugar a otro radical cuyo índice es igual a la multiplicación de los índices de cada uno de los radicales.
Raíz de una potencia
Al contrario que en el caso anterior, la raíz de una potencia es igual a otra raíz con un índice que se obtiene de dividir el índice de la raíz entre el exponente de la potencia. Si coinciden el índice y el exponente nos quedamos con el número simplificado al máximo.
Potencia de un radical
La potencia de una raíz es igual al radical de ese número elevado a la potencia que se elevaba el conjunto del radical.