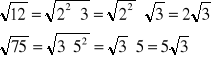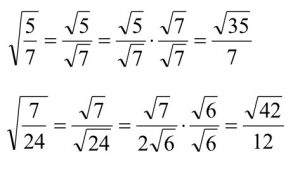¿En qué consiste la simplificación de los radicales?

La simplificación de radicales es, sin lugar a dudas, una de las operaciones con radicales más habituales en los problemas matemáticos. Este ejercicio no es más que un método empleado para demostrar las propiedades matemáticas específicas de este tipo de operación. ¿Quieres saber cómo simplificar radicales? Presta especial atención.

Proceso para simplificar radicales

El concepto de simplificar radicales consiste en transformar una expresión algebraica que sea compleja en la forma equivalente más sencilla. De forma convencional, se suele considerar que los radicales deben expresarse en su forma más sencilla. Además, también nos permite, en muchas ocasiones, obtener radicales semejantes que necesitamos para alguna operaciones. Se considera que se ha conseguido la forma más simple de un radical cuando:

• El radicando no tiene ningún factor o su exponenente es menor que el índice del radical
• El radicando no posee fracciones
• El denominador no posee radicales
• El índice del radical es el más pequeño de todos los radicales equivalentes

Una de las propiedades de los radicales es que se pueden multiplicar y dividir por el mismo número sin que varíe el resultado. Por ello, se utiliza esta propiedad para conseguir simplificar los radicales al máximo, de forma que se convierten en una expresión algebraica mucho más sencilla a la vista. Existen multitud de procesos para la simplificación de radicales paso a paso según cómo sea el tipo de expresión que nos encontramos.

Simplificación de radicales: ejercicios resueltos

En este apartado podrás ver algunos ejemplos de simplificación de radicales online, con los que podrás entender a la perfección en qué consiste conseguir el radical más sencillo. Sin embargo, hay muchos más que debemos realizar basándonos en las propiedades de los radicales.

Aquí podemos ver algunos ejercicios resueltos de simplificación de radicales. Para ello, se separan los factores que existen dentro del radicando para reducir al máximo la expresión en cuestión. Los resultados que encontramos ya no pueden simplificarse más porque son números primos, y no se puede extraer la raíz de ellos.

En este otro ejemplo vemos cómo simplificar radicales con fracciones. Para ello, debemos separar el numerador y denominador, colocándolos en radicales distintos, y reducirlos al máximo. Después debemos racionalizar la fracción, que consiste en multiplicar la fracción por el radical que tengamos en el denominador para hacerlo desaparecer.