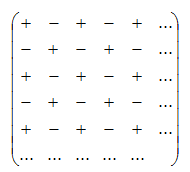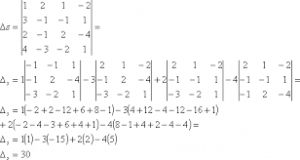- ¿Cuántos tipos de matrices existen en el álgebra?
- ¿Cómo se resuelven las operaciones con matrices?
- Matriz inversa
Los determinantes de las matrices son muy importantes ya que tienen mucha utilidad a la hora de realizar ejercicios y problemas de matemáticas. En este caso, podrás utilizar la calculadora de matrices para calcular el determinante de la matriz 4x4 online y comprobar tus resultados al instante.
No te preocupes si no puedes utilizar la calculadora para tus operaciones con matrices, ya que aquí enseñamos en qué consisten los determinantes de una matriz y cómo se calcula el determinante de una matriz por adjuntos.
¿Qué es el determinante de una matriz?
El determinante de una matriz se define como un número escalar que tiene cada una de las matrices cuadradas que existen. Hablamos de matrices cuadradas cuando nos encontramos con matrices que poseen el mismo número de filas y de columnas. Debemos saber que sólo se puede calcular el determinante de las matrices cuadras.
Podemos ver el determinante de una matriz con dos expresiones diferentes como son det(A) y |A|, aunque esta última expresión no debemos confundirla con el valor absoluto de un número.
El determinante de una matriz será muy útil para calcular la matriz inversa, ya que nos indica si una matriz es invertible o no, y nos ayudará en uno de los métodos para poder calcularla.
¿Cómo se calcula el determinante de una matriz 4x4?
A pesar de que pueda parecer complicado calcular el determinante de una matriz 4x4, tenemos que tener en cuenta que es muy sencillo si comprendemos cómo hacerlo. Muchos lo consideran un proceso lioso, por lo que debemos estar atentos a cada uno de los pasos que realizamos para obtener el determinante.
La regla de Sarrus, no nos permite encontrar el resultado del determinante de una matriz 4x4, ya que solamente sirve para las matrices cuadradas de orden 3. Por ello, vamos a aprender cómo obtener el determinante de una matriz 4x4 por adjuntos paso a paso.
Primero, tenemos que observar si existe alguna fila o columna que posea uno o más 0. Si existe, escogeremos la que más 0 posea, ya que esto nos ayudará a reducir las operaciones que tenemos que hacer. En el caso contrario, podemos elegir la fila o columna que queramos.
Después multiplicaremos cada número de la fila o columna que hayamos elegido por el determinante adjunto, que es el determinante resultante de eliminar la fila y la columna en la que se encuentra el número. Debemos tener en cuenta el signo de cada número según la posición que ocupa en la matriz. En esta imagen puedes ver cuáles son los signos que le pertenece a cada posición de la matriz.
Para que puedas entender perfectamente cómo se calcula el determinante por adjuntos vamos a repasar el cálculo paso a paso a través de la imagen. Antes que nada, como no había ninguna línea con 0, hemos escogido la primera columna.
Después hemos cogido el primer número de la columna (1), en signo positivo porque es la primera posición, y lo hemos multiplicado por el determinante de su adjunto, que es el determinante de la matriz que surge al eliminar la primer fila y la primera columna, que son las líneas a la que pertenece. Luego hemos hecho lo mismo con cada uno de los número de la primera columna. Debes fijarte en que hemos puesto -3 y -4 porque, como vemos en la imagen de arriba, es el signo que les pertenece por su posición en la matriz.
Ahora que ya tenemos expuestos los determinantes adjuntos, tenemos que calcularlos para poder obtener el resultado. Tendremos que utilizar la regla de Sarrus para calcular el determinante de 3x3. Después de ello, solo nos queda sumar todos los elementos y este será el resultado del determinante.