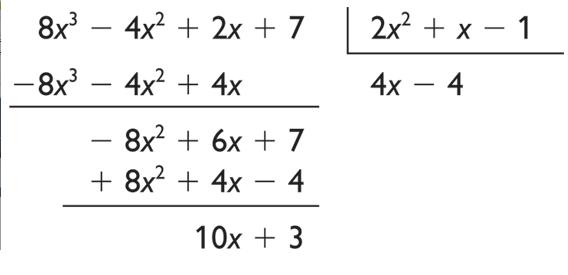¿Cómo resolver operaciones con polinomios?

Ahora que conocemos los distintos tipos de polinomios que existen en el álgebra, no está de más que tengamos en cuenta las operaciones con polinomios que podemos encontrar en nuestros ejercicios de matemáticas. ¿Quieres aprender a resolver operaciones con polinomios? Aquí te enseñamos cómo hacerlas.

Operaciones con polinomios

Si ya somos capaces de identificar cómo se clasifican los diferentes tipos de polinomios, ahora toca descubrir la forma en que se realizan las diferentes operaciones con polinomios que existen. Para dar un paso adelante en esta parte tan interesante del álgebra, conoce qué debes hacer en cada momento, con las operaciones con polinomios resueltas que tienes a continuación.

Suma de polinomios

Cuando sumamos diferentes polinomios debemos sumar los coeficientes que tengan el mismo grado, es decir, que sólo podemos sumar coeficientes que tengan el mismo exponente. Por ello, es conveniente ordenar los números para que sea mucho más fácil realizar la suma.

P(x)

= 5x³ + 2x − 3

Q(x)

= 2x − 5x² + x³

P(x) + Q(x)

= (5x³ + 2x − 3) + (x³ − 5x²+ 2x) = 5x³ + x³ − 5 x² + 2x + 2x − 3

P(x) + Q(x)

= 6x³ − 5 x² + 4x − 3

Recapitulando, debemos primero ordenar los coeficientes del mismo grado. Después debemos sumar los coeficientes del mismo grado respetando los signos que poseen. Finalmente, obtendremos el polinomio final que resulta de sumar los dos anteriores.

Resta de polinomios

La resta de polinomios se realiza mediante el mismo proceso que la suma de polinomios pero restando el sustraendo al minuendo, o lo que es lo mismo, sumando al primer polinomio el opuesto del segundo. Cabe recordar que hay que ir con cuidado con los signos, ya que cuando restamos un número negativo se convierte en una suma. Puedes verlo en estos ejemplos de operaciones con polinomios.

P(x) − Q(x)

= (4x³ + 6x − 2) − (3x³ − 2x² + 3x)

P(x) − Q(x)

= 4x³ +6x − 2 − 3x³ + 2x² − 3x

P(x) − Q(x)

= 4x³ − 3x³ + 2x² + 6x − 3x − 2

P(x) − Q(x)

= x³ + 2x² + 3x − 2

Tal y como hemos hecho con la suma, primero debemos ordenar los polinomios del mismo grado para después poder restarlos.

Multiplicación de polinomios

Existen diversas operaciones de multiplicaciones con polinomios:

Multiplicación de un número por un polinomio

Cuando multiplicamos un número natural por un polinomio se multiplica el número por cada una de la unidades de cada monomio, y se respeta el mismo exponente. De esta forma seguimos teniendo un polinomio del mismo grado.

2 · (4x³ − 2x² + 3x − 5) = 8x³ − 4x² + 6x − 10

Multiplicación de un monomio por un polinomio

En este tipo de operaciones debemos multiplicar el monomio por cada uno de los monomios que forman el siguiente polinomio. Cuando multiplicamos diferentes monomios debemos multiplicar las unidades que la forman y sumar los exponentes que poseen. Averigua cómo resolver estas operaciones con polinomios. Por ejemplo: 4x² · 2x³ = 8x⁵

P(x) · Q(x) =2x² · (2x³ − 5x² + 7x + 4) = 4x⁵− 10x⁴ + 14x³ − 8x²

Así, hemos multiplicado 2x²  por todos los elementos del polinomio.

Multiplicación de polinomios

Para llevar a cabo esta operación debemos multiplicar cada uno de los monomios del primer polinomio, por todos los elementos del segundo polinomio. Después debemos sumar todos los monomios que posean el mismo coeficiente y obtendremos el polinomio resultante. Con estos ejemplos entenderás la explicación de las operaciones con polinomios.

P(x) · Q(x) = (3x² − 2) · (3x³ − 4x² + 2x) = 9x⁵ − 12x⁴ + 6x³ − 6x³+ 8x² − 4x

P(x) · Q(x) = 9x⁵ − 12x⁴ + 8x² − 4x

Después de multiplicar y sumar nos sale un polinomio de grado 5, que es la suma de los grados de los polinomios que se han multiplicado 3x² − 2 (grado 2) y 3x³ − 4x² + 2x (grado 3). Esto nos puede ayudar para saber si hemos realizado correctamente la operación.

División de polimonios

Para realizar la división debemos colocar a la izquierda el dividendo y a la derecha el divisor, tal y como se hacen las divisiones tradicionales. Para empezar hay que dividir el primer monomio del dividendo entre el primer monomio del divisor (8x³ : 2x²) y el resultado los ponemos como el primer número del cociente (4x). Después multiplicamos este número del cociente por el divisor y se lo restamos al dividendo. Estos ejercicios resueltos de división de polinomios te ayudarán a entender cómo se hacen.

Con el resultado que nos da esta resta, volvemos a realizar la misma operación hasta que se nos quede un resto formado por un polinomio de menor grado que el divisor. En este caso 10x + 3 es el resto porque es un polinomio de primer grado, mientras que el divisor es de segundo grado.