- ¿Qué es el límite de una sucesión?
- ¿Cuántos tipos de sucesiones existen en el álgebra?
- ¿Sucesión y progresión aritmética es lo mismo?
Aunque todas las sucesiones matemáticas sean conjuntos de elementos dispuestos de forma ordenada, existen diversos tipos de sucesiones que debes conocer. La clasificación de las sucesiones depende, entre otros factores, de la disposición de los elementos en la sucesión y del límite de la sucesión en sí. ¿Quieres saber cuántos tipos de sucesiones existen en el álgebra? Presta especial atención.
Clases de sucesiones algebraicas
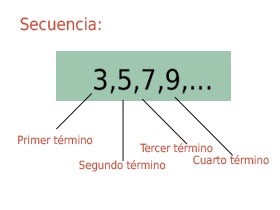
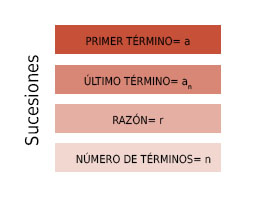
Una sucesión (an) es un grupo de elementos, normalmente números, que están colocados de forma ordenada siguiendo una aplicación lógica. Estas aplicaciones pueden ser incontables, pero se pueden agrupar en diferentes tipos de sucesiones según cómo esté formado el conjunto y del límite de términos que pueda contener.
En primer lugar todas las sucesiones pueden ser finita o infinita,a partir de esta primera clasificación, se van definiendo el resto:
- Sucesión finita: es una sucesión, una serie de elementos que tienen un final. El primer y último número ya están definidos.
- Sucesión infinita: son aquellas sucesiones que no tienen un final y siempre se distinguen por ir seguido de los tres puntos (...).
Una vez entendida esta clasificación de sucesiones algebraicas más general, profundizamos en los distintos tipos de sucesiones matemáticas definiendo cada una:
1. Sucesiones convergentes
Este tipo corresponde a las sucesiones con límite finito. Podemos decir que converge a '0' o a '1'.
- La sucesión an = 1/n converge a 0. Por ejemplo:
1, 1/2, 1/3, 1/4, 1/5..., 1/n
- La sucesión an = n/n+1 converge a 1.Por ejemplo:
1/2, 2/3, 3/4, 4/5, ..., n/n+1
2. Sucesiones divergentes
Este tipo de sucesión algebraica es de límite infinito. Se representa con el símbolo del infinito (∞) o tres puntos suspensivos.
- La fórmula es 2n+3, por ejemplo:
5, 7, 9, 11, 13, 2n+3
3. Sucesiones oscilantes
Estas sucesiones no son ni convergentes, ni divergentes, se alterna de mayor a menor y viceversa. Por ejemplo:
1, 0, 3, 0, 5, 0, 7, ...
4. Sucesiones alternadas
Estas sucesiones hacen a su vez otra clasificación de sucesiones numéricas- convergentes, divergentes y oscilantes- y son aquellas que alternan los signos de sus términos o números.
- Sucesiones alternadas convergentes: Son aquellas que tienen límite=0 sean pares o impares.
1, −1, 0.5, −0.5, 0.25, −0.25, 0.125, −0.125,..
- Sucesiones alternadas divergentes: cuando tanto términos pares o impares su límite=∞.
1, 1, 2, 4, 3, 9, 4, 16, 5, 25, …
- Sucesiones alternadas oscilantes: son las series en las que se cumple la siguiente fórmula: (−1)n n
−1, 2, −3, 4 ,−5, …, (−1)n n
5. Sucesiones monótonas
Las sucesiones monótonas se clasifican en sucesiones monótonas crecientes y decrecientes. Por tanto, estas serie numéricas se dan cuando los términos de la sucesión crecen y decrecen. Crecientes sería cuando cada uno de los números es igual o menor que el que le sigue. Y. decreciente lo contrario, cuando los números son mayores o iguales que el siguiente.
Creciente: ann < ó = an +1
Decreciente: an > ó = an+ 1
6. Sucesiones acotadas
Se dice que es una sucesión acotada cuando la serie ha de estar comprendida entre dos número definidos, llamemos los 'k' y 'K'. Existen dos tipos de sucesiones acotadas en álgebra según el número que limita la secuencia:
- Secuencia acotada superiormente: Se define cuando todos los númros son iguales o mayores a un número La fórmula es :
an ≤ K.
- Secuencia acotada inferiormente: Cuando todos los términos son iguales o menores a un número K. Este número se nombra como cota inferior.
k ≤ an ≤ K