¿Qué es el límite de una sucesión?

¿Sabías que las sucesiones numéricas no pueden entenderse sin el estudio del límite de una sucesión? Aunque las sucesiones matemáticas sean conjuntos de números dispuestos de forma ordenada, si no sabemos qué es el límite de una sucesión y no lo calculamos de forma adecuada, difícilmente podremos conocer el tipo de sucesión que tenemos ante nosotros. ¿Quieres saber a qué llamamos límite de una sucesión exactamente? No dudes en seguir leyendo.

¿En qué consiste el límite de una sucesión?

El límite de una sucesión es el valor al cuál se pueden aproximar las cantidades de serie numérica como máximo. Dicho de otra forma, es la cantidad que pone límite a la sucesión de valores. Algunos de los tipos de sucesiones que existen en álgebra tienen límite finito, se llaman sucesiones convergentes y otros tienen límite infinito, son sucesiones divergentes. Expliquemos cuál es el límite de una sucesión con términos matemáticos, paso por paso:

• Una sucesión genérica se simboliza como a_n. El subíndice (n) nos dice el lugar que ocupa el término en la sucesión. Por ejemplo: a5  significa que es el quinto término de la sucesión.
• Las sucesiones en álgebra pueden tener tantos números naturales como haya, por tanto, en general una sucesión tiene una cantidad infinita de términos.
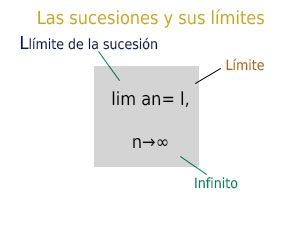
• A partir de aquí, ¿cómo se determina el límite de una sucesión? Para calcular el límite (l) de la sucesión (lim a_n) tenemos que encontrar a qué número, si es que existe, se aproximan los números o términos.
• Entonces, si tenemos  sucesión a_n que tiene por límite (l), tiende a 'l' o converge a 'l' cuando 'n' tiende a infinito (∞), y se simbolizará:

Ejemplos de límites de sucesiones

Para entender mejor a las sucesiones y sus límites, ponemos un ejemplo de sucesión convergente con límite 0, otra de límite 1 y un ejemplo de límite de sucesión infinito, en este caso de sucesión divergente:

• Límite 0: 1, 1/2, 1/3, 1/4, 1/5..., 1/n

a₁= 1

a₂= 0.5

a₁₀₀₀= 0.001

a_1000.000 = 0.000001

• Límite 1: 1/2, 2/3, 3/4, 4/5, ..., n/n+1

a₁= 0.5

a₂= 0.6666....

a₁₀₀₀= 0.999000999001

a_1000.000 = 0.999999000001

• Límite ∞: 5, 7, 9, 11, 13, 2n+3

a₁= 5

a₂= 7

a₁₀₀₀= 2.003

a_1000.000 = 2.000.003