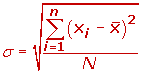- La media aritmética
- La moda en estadística
- La mediana en estadística
- La varianza en estadística
- La desviación típica
- Ejercicios de media aritmética
- Ejercicios de moda en estadística
- Ejercicios de desviación típica
- Ejercicios de mediana en estadística
La desviación estándar es un concepto difícil de entender en estadística, siendo una medida de dispersión calculada a partir de la varianza. Si queremos saber cómo calcular la desviación típica, lo primero que debemos conocer es su fórmula y tener la calculadora de desviación típica a mano para resolver los ejercicios y problemas matemáticos.
La desviación típica nos ayudará a saber explicar cómo están de lejos ciertos puntos de datos, sin tener que hacer un cálculo aproximado. Por ello, saber cómo calcular la desviación estándar será un componente necesario para descifrar las actividades que nos planteen.
Cálculo de la desviación estándar paso a paso
Para realizar el cálculo de la desviación estándar podremos seguir los siguientes pasos para conseguir los resultados deseados:
- Calcular la media de los números
- Restar la media a cada número y elevarlo al cuadrado
- Calcular la media de esas diferencias de cuadrado
Al obtener la varianza, realizaremos la raíz cuadrada de la misma obteniendo así la desviación estándar de los datos.
Ejemplos de desviación típica
Un ejemplo de desviación típica será el que detallamos a continuación:
Le preguntamos a 40 personas el número de miembros que forman parte de la unidad familiar obteniéndose los siguientes resultados:
Número de personas 2 3 4 5 6 7
Frecuencia 4 11 11 6 6 2
Para conseguir el cálculo de la desviación típica realizaremos la siguiente tabla de frecuencia donde:
- Fi es la frecuencia absoluta acumulada la necesitamos para calcular la mediana.
- xi·fi es el sumatorio de esta columna para la fórmula de la media aritmética. Los valores se hallan multiplicando xi·fi de cada fila.
- xi2·fi es el sumatorio para hallar la desviación típica. Para conseguir los valores se multiplica en cada fila el valor de xi por xi·fi.
| Tabla para calcular la media y desviación típica | ||||
|---|---|---|---|---|
| personas xi | frecuencia fi | Fi | xi · fi | xi2 · fi |
| 2 | 4 | 4 | 8 | 16 |
| 3 | 11 | 15 | 33 | 99 |
| 4 | 11 | 26 | 44 | 176 |
| 5 | 6 | 32 | 30 | 150 |
| 6 | 6 | 38 | 36 | 216 |
| 7 | 2 | 40 | 14 | 98 |
| ∑ | 40 | 165 | 755 | |