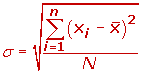- La media aritmética
- La moda en estadística
- La mediana en estadística
- La varianza en estadística
- La desviación típica
- Ejercicios de media aritmética
- Ejercicios de moda en estadística
- Ejercicios de desviación típica
- Ejercicios de mediana en estadística
La desviación típica es la raíz cuadrada de la varianza, siendo la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación. La desviación típica es representada por el siguiente símbolo de la desviación estándar σ.
Entonces para calcular la desviación típica, primero obtendremos la varianza en estadística siguiendo los pasos enumerados a continuación:
- Calcular la media de los números
- Restar la media a cada número y elevarlo al cuadrado
- Calcular la media de esas diferencias de cuadrado
Después de obtener la varianza, realizaremos la raíz cuadrada de la misma obteniendo así la desviación estándar de los datos.
Ejemplos de desviación típica
Deberemos tener en cuenta que la desviación típica será siempre un valor positivo o cero y que si a todos los valores le sumamos un número, la desviación típica no varia. A continuación, veremos un ejemplo de desviación típica a partir de una tabla para calcular la desviación estándar de manera correcta.
| xi | fi | xi· fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
Fórmula de la desviación típica
Fórmula de la desviación estándar simplificada
