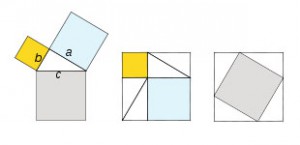
La demostración del Teorema de Pitágoras por Euclides, es otra de las demostraciones que exponen la proporcionalidad de los lados entre los triángulos rectángulo y demuestran que gracias a estas proporciones podemos emplear su aplicación para resolver distintos problemas relacionados con geometría. Pero para entender esto, primero tenemos que tener claro qué es el Teorema de Pitágoras.
Así pues, el Teorema de Pitagoras, es una teoría formulada por un conocido filósofo Pitágoras y sus seguidores, los pitagóricos, que gira entorno a la relación existente entre los lados de los triángulo rectángulo. A lo largo de la historia del Teorema de Pitágoras han ido apareciendo muchas teorías sobre su aplicación de la mano de diferentes filósofos y matemáticos, pero no todas fueron válidas y llegaron hasta nuestros días. Sin embargo, Euclides pudo hacerse un hueco en su historia y dar base a su teoría.
La demostración de Euclides se basa en:
- La construcción de cuadrados sobre segmentos
- Los ángulos adyacentes suman dos rectos.
- Es el primer teorema de congruencia entre triángulos.
- La relación entre triángulos y paralelogramos con la misma base y paralela.
Podemos decir que la demostración de Euclides sobre el Teorema de Pitágoras tiene una aplicación firmemente geométrica, puesto que solo es aplicable en los triángulos rectángulos para resolver problemas sujetos a las proporcionalidades de dichos triángulos. Ésta crea una secuencia de construcciones mediante las congruencias de triángulos, así se forman unos cuadrados sobre los catetos en forma de rectángulo que al encajarse con la hipotenusa crean el cuadrado.
Actualmente, aunque la demostración del Teorema por Pitágoras es la más conocida y aplicada dado que puede utilizarse para resolver otros problemas cotidianos de forma más sencilla. Euclides también es muy utilizada para resolver problemas relacionados con la geometría, sobre todo entre ingenieros, matemáticos, arquitectos etc. La principal diferencia que existe entre ambas demostraciones es que, mientras Pitágoras desarrolla su estudio teniendo en cuenta la semejanza de los lados de un triángulo rectángulo, su proporcionalidad y el tamaño de las áreas, Euclides, se centra en las áreas que componen un triángulo y expone que el área del cuadrado de la hipotenusa es igual a la suma de las áreas de los catetos.