Ecuaciones de tercer grado

Las ecuaciones de tercer grado se representan con la fórmula ax³+bx²+cx+d=0 y también son llamadas ecuaciones cúbicas, donde una de las incógnitas será de tercer grado. Este tipo de ecuaciones se podrán resolver siguiendo una serie de pasos que explicaremos a continuación.

Ecuaciones de tercer grado paso a paso

Cuando nos encontramos con una ecuación cúbica o de cualquier grado escrita de la forma P(x)=0 podemos pensar que es difícil pero si queremos resolver las ecuaciones de tercer grado paso a paso sólo tendremos que seguir las siguientes instrucciones aplicando la regla de Ruffini correctamente partiendo de la siguiente ecuación cúbica 2x³-7x²+8x-3=0

• Buscar los divisores del término independiente. El término independiente es -3 y los divisores de -3 son 1, -1, 3 y -3
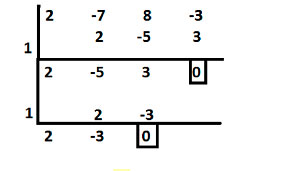
• Hacemos las divisiones por Ruffini con los divisores

• Al ser Sacamos las raíces del polinomio

(x-1)(x-1)(2x-3)

• Igualamos los binomios a cero para formar ecuaciones y encontrar las soluciones.

x-1=0;x=2

2x-3=0;2x=3;x=3/2

Fórmula ecuaciones de tercer grado